Table of Contents
Toggle
It’s time to understand the mutual fund’s risk ratios calculation. In our previous topics, we have clearly explained the basic concepts of mutual funds. We know the calculation of financial ratios and the qualitative approach in equity investment.
Coming to mutual fund investments, we only rely on the past returns of the funds, and based on that we make a decision. This is not the correct method to select the mutual fund scheme. Here we try to explain some of the alternative methods to select the fund based on the risk ratios of the mutual fund.
Mutual fund risk ratios give a clear picture of the mutual fund return, even fund managers make an investment decision based on the risk ratios. Investors need to understand the risks before making an investment decision.
What is Risk Ratios in Mutual Funds
Risk is defined as a deviation from expectation. Deviation from expected outcomes can be positive or negative but as an investor, we are very cautious about downside risk in the market.
As we know mutual fund house collects the fund from the investors and invest in different financial instruments like equity, bonds, and government securities. Since mutual fund schemes invest in the markets, the return they will earn is unpredictable.
In the market, such risk is quantified through the following ratios
- Standard deviation
- Beta
- Alpha
- Sharp Ratio
Let us have a quick view of the above ratios
Standard Deviation:
The standard deviation is the average deviation of observed returns from the average return over some time.
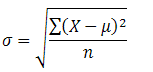
Where
X = yearly return of the fund
µ = average return of the fund
N= number of years (mostly take data for the last ten years from fund inception)
Standard deviation measures dispersion, how much the fund will scatter away from the average return. Remember one thing, higher standard deviation means, the fund is considered high risk.
Alpha:
Simply stated, “Alpha is the excess return relative to benchmark index return”. For example, if an asset manager gets a 12% return in a specific mutual fund against a benchmark index of 10%, that means the alpha ratio would be 2. An alpha of 2.0 means the fund has outperformed its benchmark index by 2%. For investors, the higher the alpha is considered for investment.
Beta:
Beta is a measure of the volatility of a security or portfolio in comparison to the market as a whole. By definition, the market has a beta of 1.0. If any individual stock or fund portfolio has more than 1.0 indicates that the fund will be more volatile than the market.
For example, if a fund portfolio beta is 1.3, it means the fund has 30% more volatility than the market. If a scheme outperformed its benchmark index, we should understand, whether the beta of the scheme was high or the fund manager was able to deliver better returns.
Calculation of Mutual Funds Risk Ratios:
To understand alpha and beta, we just need a basic understanding of the Capital Asset Pricing Model (CAPM).
It simply explained the relationship between fund returns and market risk. The mathematical equation of the CAPM is as follows
Fund Return = Risk free rate + Beta * (benchmark return – risk free rate)
*For the risk-free rate, we can consider the ten-year government bond yield or fixed deposit return of the nationalized banks. It’s also called the expected return of the fund.
Let’s calculate the Alpha of the portfolio from the above calculation
Alpha of portfolio = Actual return of portfolio – An expected rate of return on the portfolio
The actual return of the fund may be varied from our expected return. The difference in actual return and expected return is known as Alpha in mutual funds. The mathematical equation for alpha is
Fund Return = Risk free rate + Beta * (benchmark return – risk free rate) + Alpha
Almost we understand the calculation of Alpha, let’s go to the calculation of beta
The beta of Mutual funds = Covariance / Variance of market return
These are the statistical terms, try to understand the difference first.
Covariance measures the total variation of two random variables from their expected values. Variance measures the variation from the mean value.
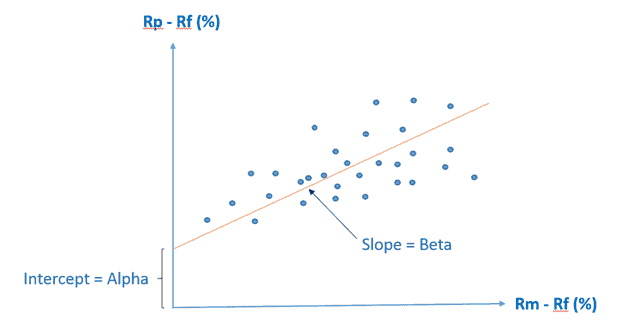
Let us correlate these statistical terms with mutual funds
Beta is calculated statistically by fitting a line through a plot of the excess return of the fund over a risk-free rate in the Y-axis versus the excess return of benchmark index return (Rm) over a risk-free rate.
The slope or gradient of the best fit line through this plot is the beta of the fund.
Conclusion:
- Standard deviation tells us how much return on a fund is deviating from the expected returns based on the historical performance.
- The higher the alpha ratio in mutual fund schemes consistently, the higher the possibility of long-term returns
- Anything more than zero is a good Alpha
- Generally, a Beta of around 1 or less is recommended.
- If our fund beta is more than 1, then make sure that we are comfortable with the risk, as per our risk-taking capacity.